"What I cannot create, I do not understand"
On the last blackboards of Richard Feynman:
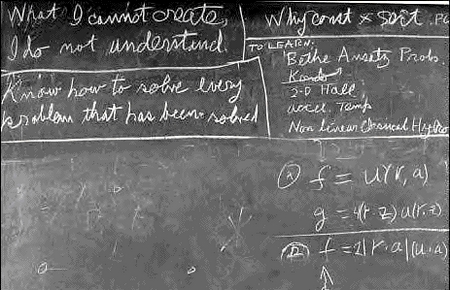 [more]
[more]
Consider, for a moment, the core verbs of participation on the web today. I’m not talking about GET or POST. I’m talking about CREATE, REMIX, SHARE, and DISCUSS. Am I forgetting any? Each of these represents a form of engagement that is meaningful – and near-ubiquitous – for most any website built around “user-generated content” (I triple-shudder on that phrase.) While Sketchpad is still embarrassingly-deficient on letting people DISCUSS (stay tuned…), I’ve taken a slight detour to test out a new verb: RECREATE. This is not a general-purpose verb, but I think it’s worth trying out on Sketchpad and sites like it, where there’s interest in supporting learning and teaching.
In basketball, you’ve got games like H-O-R-S-E. In art studios, you’ve got people attempting to replicate a masterpiece or copy a style. In music lessons, you’ve got students trying to repeat back what they hear their teachers play. I’m wondering if these types of learning exercises might make sense for creating things on the web. I can’t think of any examples of sites that support RECREATE as a top-level verb, so I thought I’d try it out right here on Sketchpad.
As of earlier today, every sketch has a little “recreate” link in the footer, giving you an entry-point to do just that. Click on it, and you’ll be given a blank canvas, the sketch editor, and the masterpiece of your choosing (drawn from any revision of any sketch found on the site). You can take a totally different path than the creator did, but the idea is to arrive at a finished version as close to the original as possible. Try your hand at making this tic-tac-toe game:
Or replicating this bit of recursion:
This is a brand-new experiment. I’m not sure if anyone will use it, so I’ll wait a bit to see. I the meantime, I’m adding it to the list of useful techniques for teaching with Sketchpad. If you’re an educator interested in testing this out, please let me know!